Una paradoja matemática del tablero de ajedrez
El Ministerio Federal de Investigación y Ciencia proclamó 2008 como “Año de las Matemáticas”. Además, en 2008 se disputaron un Campeonato del Mundo de Ajedrez y una Olimpiada de Ajedrez, así que también se podría pensar en 2008 como el “Año del Ajedrez”. Eso facilita razones más que suficientes para mirar un interesante problema en la interfaz de esas dos actividades intelectuales: matemáticas y ajedrez. Es una paradoja fascinante que parece demostrar que 64 es igual a 65 con solo cortar el tablero de ajedrez (que, por supuesto, tiene 64 casillas) en cuatro piezas y ensamblarlas en un rectángulo cuyos lados tienen 5 y 13 casillas respectivamente (lo que, por supuesto, da un área de 5 x 13 = 65 casillas)
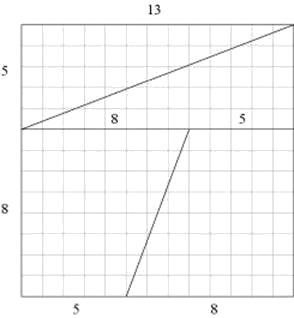
En concreto lo que tengo en la mente es esto:
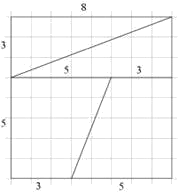
Con tres cortes directos, el tablero de ajedrez ha sido diseccionado en dos triángulos iguales y en dos trapezoides iguales. La suma de las áreas de esas esas 4 piezas es de 64 casillas del tablero de ajedrez. Esas cuatro figuras geométricas diseccionadas del tablero pueden ahora ensamblarse para que formen el siguiente rectángulo:
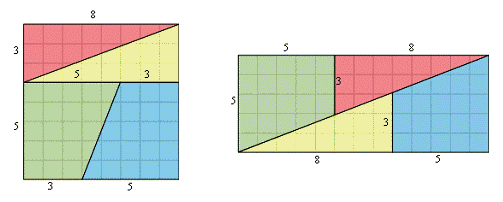
Por favor, comparen cada una de las cuatro piezas de los dos diagramas. Los bordes del rectángulo resultante constan de 5 y (8+5) = 13 casillas. Entonces el área del rectángulo es de 5 x 13 = 65 casillas. Son las mismas cuatro piezas recortadas del tablero de ajedrez, solo que dispuestas de forma diferente, por lo que el área total debería ser la misma.
Por lo tanto parece que hemos probado que ¡64 = 65! Por supuesto, eso no es cierto y debe haber algún error en algún sitio. ¿Puede localizarlo?
Lo que subyace como clave de la paradoja anterior son las inexactitudes al dibujar las líneas de forman los triángulos y los trapezoides y, con ello, el rectángulo. Presentado con una resolución mayor, el diagrama anterior sería algo como:
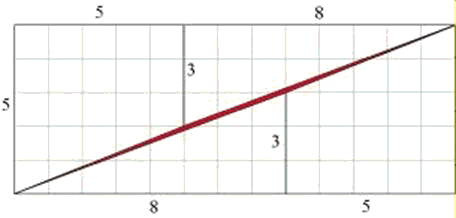
Y ampliando aún más la zona central se ve con más claridad la escisión entre las partes.
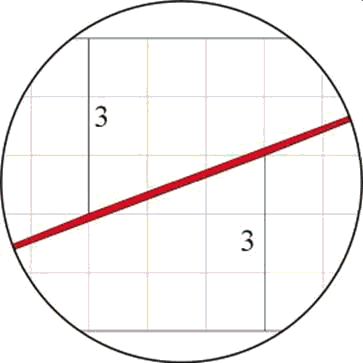
El área resaltada en rojo en los diagramas anteriores tiene la forma de un paralelogramo muy largo. Es el responsable de la diferencia de área entre el cuadrado y el rectángulo.
Una paradoja similar se puede construir a partir de un cuadrado de 13x13 casillas y reagrupando los dos triángulos y dos trapezoides que resultan en un rectángulo de 21x8, tal y como se hizo antes:
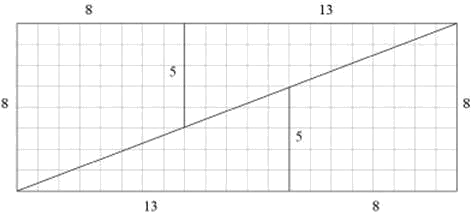
De nuevo, con mayor resolución tenemos:
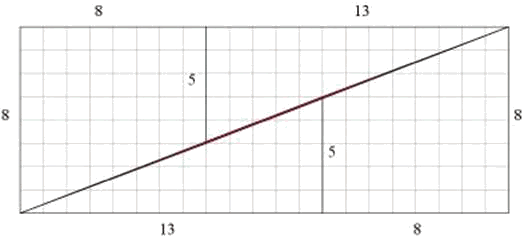
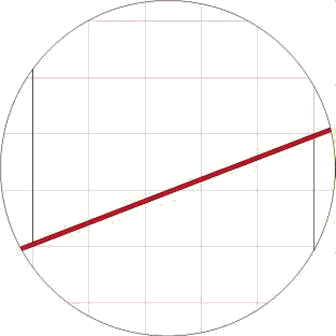
El área pintada en rojo es de nuevo un paralelogramo de área 1 en el que esta vez se solapan las partes superior e inferior. Por lo tanto en este caso, no hay escisión, sino que el rectángulo resultante tiene un área menor (=168) que el cuadrado original (=169) debido al solapamiento.
¿Cuál es el núcleo matemático de esta paradoja? Para explicarla en términos generales, comenzaremos mencionando la serie de los llamados números de Fibonacci Fn. Es una serie numérica en la que cada número Fn+1 se define como la suma de los dos inmediatos anteriores Fn y Fn-1. Por lo tanto:
Fn+1 = Fn + Fn-1 para todo n = 1, 2, 3, …
Los valores iniciales son F0 = 0 y F1 = 1. Así, los primeros valores de la serie de Fibonacci son
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
La paradoja anterior de la disección parece decir que
Fn . Fn es igual a Fn+1 . Fn-1
Hagamos unos sencillos cálculos para ver lo que pasa:
Fn . Fn = Fn(Fn-1 + Fn-2) = Fn . Fn-1 + Fn . Fn-2
y
Fn+1 . Fn-1 = (Fn + Fn-1)Fn-1 = Fn . Fn-1 + Fn-1 . Fn-1
La diferencia Dn entre esos dos productos es:
Dn = Fn+1 . Fn-1 - Fn . Fn
= Fn-1 . Fn-1 - Fn . Fn-2
= -Dn-1 = (-1)2 Dn-2 = ... = (-1)n-1D1 = (-1)n
puesto que D1 = F2 . F0 – F1 . F1 = 1 . 0 – 1 . 1 = (-1)1.
Por lo tanto hemos establecido la verdad de lo que se conoce como identidad de Cassini:
Fn+1 . Fn-1– Fn . Fn = (-1)n
La conclusión es que siempre se pueden reorganizar un cuadrado Fn x Fn en un rectángulo Fn+1 x Fn-1 y que la diferencia entre sus áreas, es decir Fn . Fn y Fn+1 . Fn-1, es (-1)n , es decir bien -1 o bien +1. En el primer caso se tiene un solapamiento entre las piezas. En el segundo caso, hay una grieta entre ellas.
El siguiente cuadrado más grande para el que funciona esta disección es de 21x21, que puede reorganizarse en un rectángulo de 34x13. Pueden figurarse como hay que cortar el cuadrado de 21x21 con solo pensar en la serie de Fibonacci.
Usted quería engañar a los bueños jijijiji